Релаксационный генератор, основанный на микросхеме таймера 555 в стандартном включении, не может обеспечить коэффициент заполнения, в точности равный 50%. Это общеизвестный факт. К счастью, есть несколько способов обойти эту проблему. Лучше всего включить дополнительный резистор R3 между точкой соединения «штатных» резисторов R1 и R2 и выводом коллектора разрядного транзистора микросхемы (Рисунок 1).

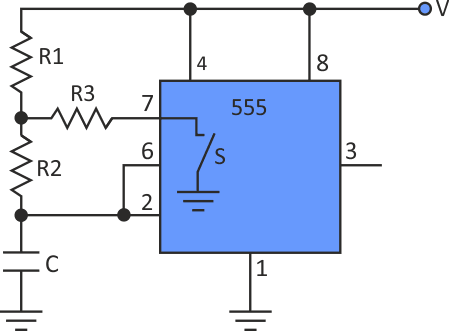Рисунок 1.	Добавление резистора R3 к стандартной схеме на таймере 555 позволяет установить коэффициент заполнения, равный 50%.

Проблема в том, что изменения сопротивления R3 сильно влияют на выходную частоту [1]. В этой статье показано, как достичь регулируемого коэффициента заполнения в 50% при минимальном изменении частоты.

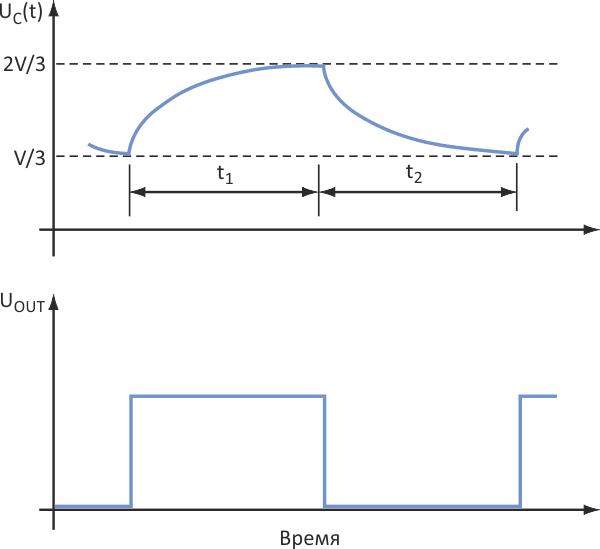Рисунок 2.	Третий резистор не влияет на нормальный цикла заряда-разряда схемы.

Даже с дополнительным резистором таймер работает в обычном режиме. Когда внутренний ключ S микросхемы разомкнут, конденсатор C заряжается через цепь R1-R2 (Рисунок 2), и напряжение на нем возрастает. Когда оно достигает 2/3 напряжения питания V, ключ замыкается, и конденсатор начинает разряжаться. Когда напряжение падает до уровня V/3, ключ размыкается опять, и цикл повторяется.

Временные интервалы t₁ и t₂ равны:

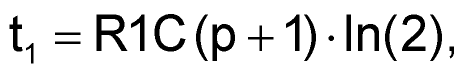(1)

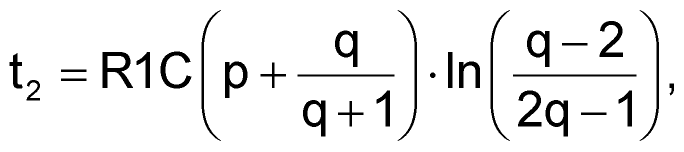(2)

где p = R2/R1 и q = R3/R1. Если коэффициент заполнения равен 50%, то t₁ = t₂, поэтому:

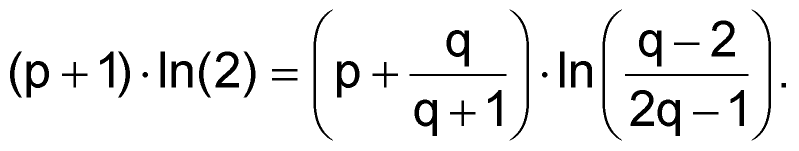(3)

А частота – это просто

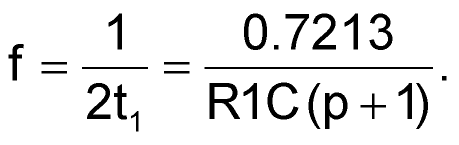(4)

Формула (3) связывает p и q. Если p задано, можно рассчитать q. Обратите внимание, что член под логарифмом в правой части формулы всегда должен быть  положительным. Это выполняется, когда и числитель, и знаменатель имеют одинаковые знаки, и это дает для q два интервала: один от 0 до 0.5, а другой от 2 до бесконечности. При этом для вычисления q можно использовать простую итеративную процедуру. Когда это будет сделано, можно будет определить R1, R2 и R3.

Процедура заключается в следующем:

1. Установите желаемую частоту и выберите значение емкости C.
2. Выберите величину p и рассчитайте q по формуле (3).
3. С помощью формулы (4) найдите сопротивление резистора R1.
4. Рассчитайте R2 = pR1.
5. Рассчитайте R3 = qR1.

В Таблице 1 приведены номинальные значения R1n, R2n и R3n, определенные с помощью этой процедуры для пяти значений p при частоте 20 кГц и емкости C, равной 1 нФ.

Таблица 1.	Зависимость сопротивлений R1, R2 и R3 от p
p R2/R1 q R3/R1 R1n (kΩ) R2n (kΩ) R3n (kΩ) 10 0.0418 3.280 32.795 0.137 5 0.0764 6.013 30.063 0.459 1 0.2248 18.038 18.038 4.055 0.1 0.3911 32.795 3.280 12.826 0.05 0.4068 34.357 1.718 13.976

Поскольку величины сопротивлений резисторов должны быть округлены до стандартных значений, коэффициент заполнения не буде равен ровно 50%. Вопрос в том, как настроить его с минимальным изменением частоты. Ответ ясен из Таблицы 2, где процентные отклонения коэффициента заполнения (duty cycle, DC) и частоты F рассчитаны для случаев, когда сопротивление одного из трех резисторов увеличивается на 5%, в то время как два других остаются неизменными. Обратите внимание, что наилучшие результаты достигаются тогда, когда для регулировки коэффициента заполнения используется R1.

Таблица 2.	Отклонения коэффициента заполнения (DC) и частоты (F) при изменениях сопротивлений
R1 = R1n + 5% R2 = R2n + 5% R3 = R3n + 5% Откл. DC (%) Откл. F (%) Откл. DC (%) Откл. F (%) Откл. DC (%) Откл. F (%) –0.44 0.01 0.21 4.56 0.24 0.24 –0.82 0.01 0.36 4.35 0.46 0.46 –2.56 –0.05 0.83 3.25 1.80 1.80 –5.52 –0.93 0.42 0.87 5.73 5.73 –6.03 –1.21 0.24 0.48 6.63 6.63

Схема, сконструированная в соответствии с описанной выше процедурой (при p = 1), была протестирована. Сопротивления резисторов были такими: R1 = 18.2 кОм, R2 = 18.2 кОм и R3 = 4.12 кОм. Затем сопротивление R1 менялось в пределах ±5%. Допускаемые отклонения номиналов всех резисторов составляли 1%. Из Таблицы 3 видно, что результаты, особенно коэффициент заполнения, были очень близки к значениям, предсказанным Таблицей 2. Они также намного лучше указанных в [1], где использовался переменный резистор R3.

Таблица 3.	Результаты испытаний схемы
R1 (кОм) DC (%) F (кГц) Откл. DC (%) Откл. F (%) 17.3 49.03 18.881 2.83 0.07 18.2 50.46 18.866 [1] [1] 19.1 51.77 18.826 –2.60 –0.22

Различия между теорией и экспериментом обусловлены допусками сопротивлений резисторов. Очевидно, что больше всего эти допуски влияют на частоту. Если требуется более точное управление частотой, можно выбрать большее значение p и/или использовать более точные резисторы. Первый вариант сужает диапазон регулировки коэффициента заполнения, а второй увеличивает цену. При необходимости частоту можно регулировать независимо от коэффициента заполнения, изменяя емкость конденсатора С.

1. Datasheet Texas Instruments LM555