Как рассчитать импульсный преобразователь электрической энергии? Часть 7
Журнал РАДИОЛОЦМАН, ноябрь 2019
Александр Русу, Одесса, Украина
Знать величины изменений токов в обмотках дросселя, безусловно, нужно, однако для выбора проводов в обмотках дросселя, впрочем, как и других силовых элементов преобразователя, этого недостаточно. Судите сами: пока мы знаем только, что ток, например, в обмотке W1 на первом этапе преобразования изменится на 3.6 А, но каково его значение было в начале этого этапа? Продолжаем разбираться.
Что нам еще известно о токах? В общем-то, немного. Нам известно, что выходные токи каналов равны IВЫХ1 = 1 А и IВЫХ2 = 1 А. Еще мы можем, приняв КПД силовой части, равным 100%, определить входной ток преобразователя IВХ:
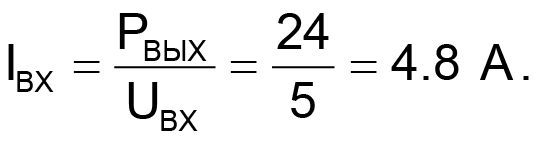 | (55) |
Но что это за токи? Поскольку конденсаторы С1 – С3 включены в схемы фильтров нижних частот и их функция, в идеале, сводится к обеспечению пути протекания для всех гармоник тока, кроме постоянной составляющей. А это означает, что токи IВХ, IВЫХ1 и IВЫХ2 есть ни что иное, как средние значения токов, в данном случае, обмотки W1 и диодов VD1 и VD2:
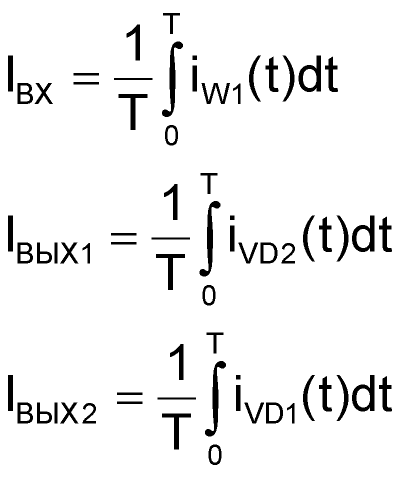 | (56) |
Но как нам узнать, по какому закону токи iW1(t), iVD1(t) и iVD2(t) изменяются во времени? Для ответа на этот вопрос лучше всего обратиться к уже известным «классическим» методам анализа электрических процессов в импульсных преобразователях.
А во многих методиках расчета принимается, что токи в силовых цепях преобразователей изменяются по линейному закону. И хотя в предыдущих частях статьи было показано, что в реальном преобразователе из-за изменения µЭКВ это может быть далеко не так, в дальнейших расчетах будет гораздо проще, если на эту нелинейность не обращать внимания. И это не просто уход от «неудобных вопросов». Как показали исследования, а импульсные преобразователи изучались не один десяток лет многими учеными, расхождения между точными моделями, учитывающими, в том числе и изменения µЭКВ, и данной «упрощенной» моделью не превышают 5%, что вполне достаточно для практики. Поэтому не будем «усложнять себе жизнь» и смело примем это допущение.
Итак, примем, что токи в обмотках дросселя изменяются линейно. Из курса математики известно, что в общем виде любая линейная функция описывается формулой:
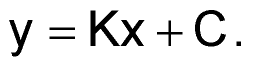 | (57) |
В данном случае, в качестве «x» у нас выступает время t, а в качестве «y» – ток i(t). Попробуем определить коэффициенты K и C. Для этого посмотрим внимательно на диаграмму тока обмотки дросселя (Рисунок 22). Как видно из графика, в общем случае она имеет два ярко выраженных линейных участка. На первом этапе преобразования (от tНАЧ1 до tКОН1) за время t1 = tКОН1 – tНАЧ1 ток изменяется на величину ΔI1 от некоторого значения IНАЧ1 до IКОН1 (ΔI1 = IКОН1 – IНАЧ1). Аналогично, на втором этапе преобразования (от tНАЧ2 до tКОН2) за время t2 = tКОН2 – tНАЧ2 ток изменяется на величину ΔI2 от некоторого значения IНАЧ2 до IКОН2 (ΔI2 = IКОН2 – IНАЧ2). Обратите внимание, что в момент переключения силовых ключей ток в обмотке дросселя может измениться скачком (этот вопрос подробно рассмотрен [12]).
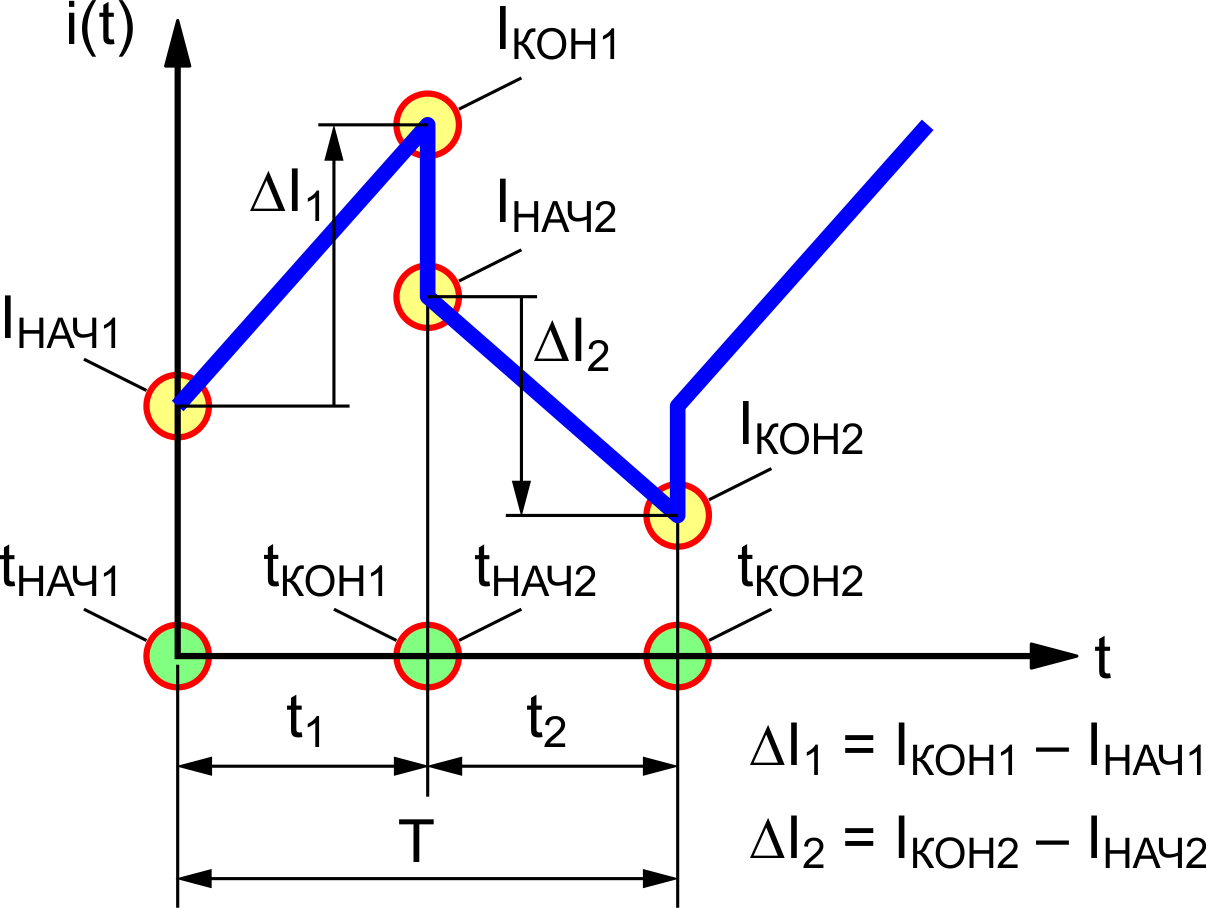 | ||
| Рисунок 22. | Ток в обмотке дросселя (общий случай). | |
Если совместить вертикальную ось воображаемой системы координат линейной функции с началом каждого из интервалов преобразования, то коэффициенты C, отвечающие за смещение графиков по вертикальной оси, будут равны IНАЧ1 (для первого интервала преобразования) и IНАЧ2 (для второго). Тогда коэффициенты K, являющиеся ни чем иными как первыми производными функции i(t) по времени, можно определить как ΔI1/t1 для первого интервала и ΔI2/t2 для второго. Следовательно, в общем виде, ток в обмотке дросселя можно записать в виде:
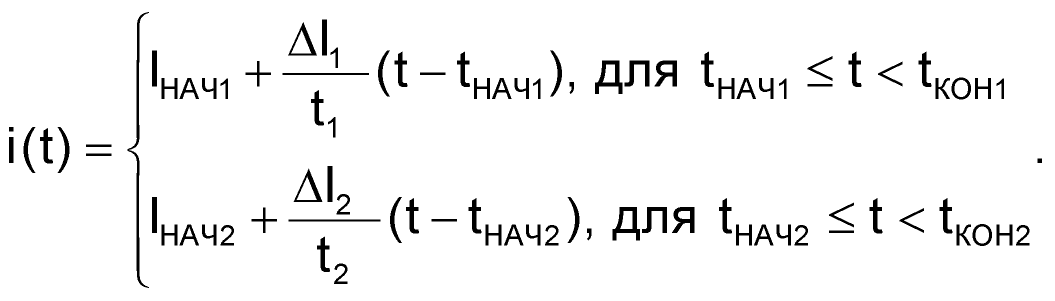 | (58) |
Формула (58) описывает ток обмотки в общем виде, и ее можно использовать в любых, даже самых «сложных» случаях, в том числе, и когда этапов преобразования больше чем два (тогда увеличится число уравнений). А теперь адаптируем ее для нашего преобразователя.
Вначале разберем более простой случай – составим уравнение для тока обмотки W2 (и диода VD1). Поскольку на первом этапе преобразования диод VD1 закрыт, и ток в этой цепи не протекает, первая строчка формулы (58) будет равна нулю. Следовательно:
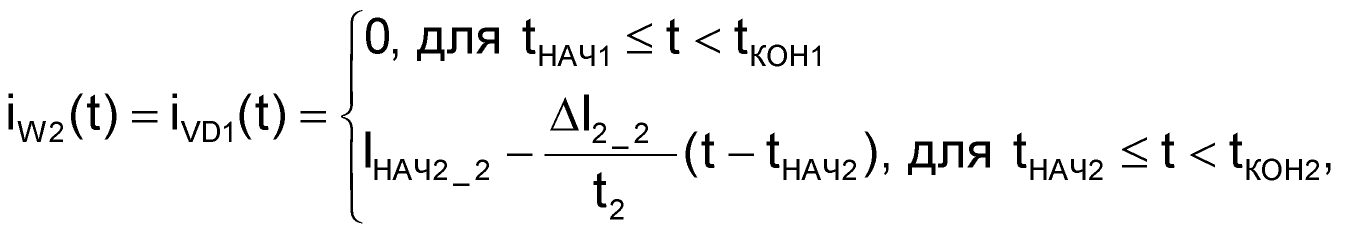 | (59) |
где
IНАЧ2_2 – ток обмотки W2 в начале второго этапа преобразования;
ΔI2_2 – изменение тока в обмотке W2 за время этого этапа.
Обратите внимание, что перед ΔI2_2 стоит знак «минус». Если подходить строго (с математической точки зрения), то в предыдущей части статьи следовало бы указать, что на втором этапе преобразования ток обмотки W2 изменится на отрицательную величину, например, на –1.53 А (т.е. уменьшится). Но тогда мы для упрощения понимания физики процессов на этот момент не обращали внимания. Но теперь настала пора это учесть, иначе потом у нас ничего не получится.
Аналогично, можно записать формулу и для тока обмотки W1, но здесь уже упрощений никаких не будет, потому что ее ток может протекать и на первом и на втором этапе преобразования:
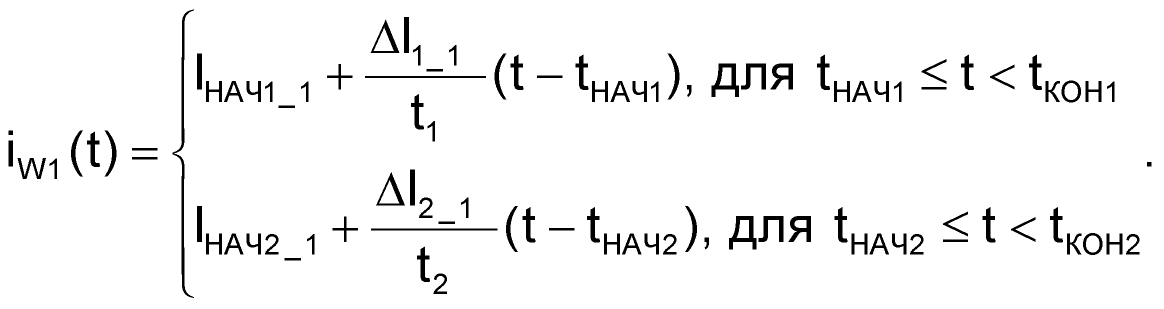 | (60) |
где
IНАЧ1_1, IНАЧ2_1 – токи обмотки W1 в начале, соответственно, первого и второго этапов преобразования;
ΔI1_1, ΔI2_1 – изменения тока в обмотке W1 за время, соответственно, первого и второго этапов преобразования.
А вот ток диода VD2, связанный с выходным током первого канала, является «обрезанной» частью тока обмотки W1, ведь на первом интервале преобразования он не протекает:
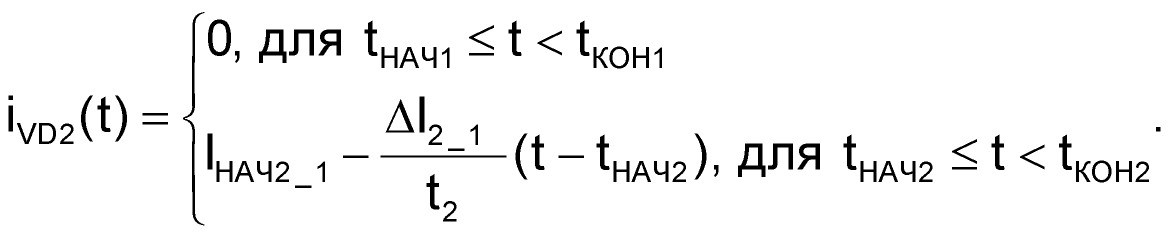 | (61) |
Изменения токов ΔI1_1, ΔI2_1, ΔI2_2 мы определи в предыдущей части статьи (Таблица 3), поэтому осталось только связать воедино формулы (56), (59) – (61) и найти «недостающие» элементы IНАЧ1_1, IНАЧ2_1 и IНАЧ2_2.
Начнем, опять же, с более простого случая – с обмотки W2. Сейчас я постараюсь максимально подробно описать последующие шаги, потому что практически все авторы на этом этапе сразу приводят готовый результат, будучи уверенными, что читатели отлично знают высшую математику. Но на самом деле такой подход приводит к тому, что приходится брать лист бумаги и, предварительно пройдя курс промышленной телепатии, заново все выводить, либо использовать готовый результат, надеясь, что он подойдет для данной задачи. В нашем случае второй вариант точно неприменим, потому что схема не является стандартной.
Итак, снова вспоминаем математику. Для начала воспользуемся свойством, что если функция интегрируема на промежутках [a, b] и [b, c], то интеграл на промежутке [a, c] можно представить в виде суммы двух интегралов:
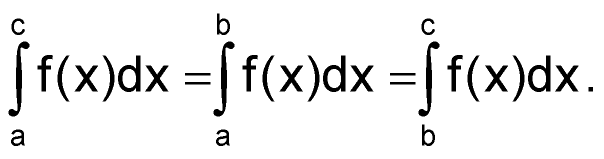 | (62) |
В нашем случае, в качестве a, b и c выступают моменты времени начала и конца первого и второго интервалов преобразования tНАЧ1, tКОН1, tНАЧ2, tКОН2, причем tКОН1 = tНАЧ2. Это позволяет записать:
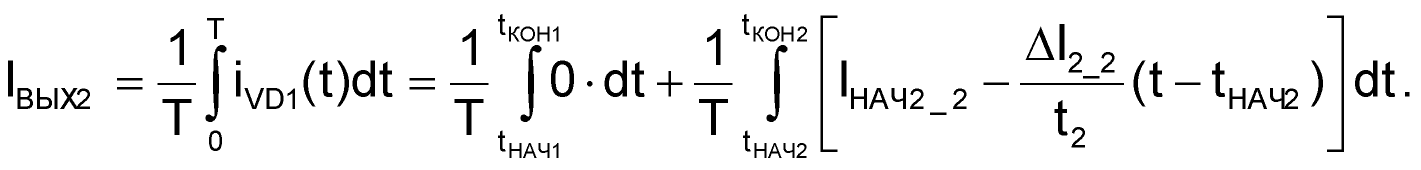 | (63) |
Первый интеграл в формуле (63) равен нулю, поэтому про него уже можно сразу забыть. А вот во втором придется раскрыть скобки, и вспомнить, что интеграл от алгебраической суммы интегрируемых функций равен алгебраической сумме интегралов:
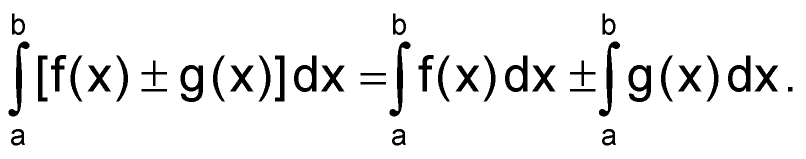 | (64) |
Тогда формула (64) примет вид (чтобы не загромождать формулу «лишними» скобками длительность периода T временно перенесем за знак равенства):
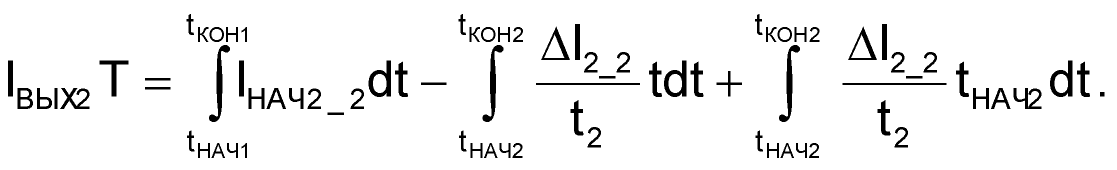 | (65) |
Поскольку все три интеграла имеют постоянные множители, то их можно вынести за знаки интегралов, воспользовавшись свойством:
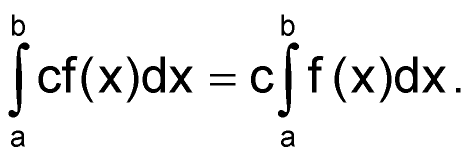 | (66) |
Тогда:
 | (67) |
«Пустые» интегралы, содержащие под знаком интегрирования лишь dt (в нашем случае – первый и третий) равны:
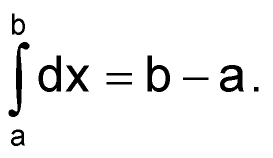 | (68) |
А вот для взятия второго слагаемого формулы (67) воспользуемся другим стандартным табличным интегралом:
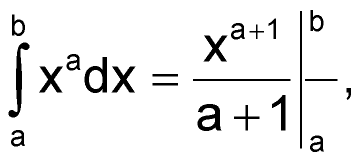 | (69) |
где показатель степени a = 1.
В итоге получим:
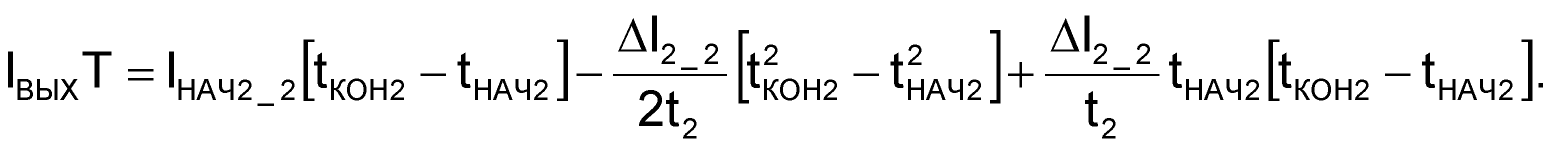 | (70) |
Для упрощения формулы (70) вспомним, что длительность второго этапа преобразования равна t2 = tКОН2 – tНАЧ2, а также распишем разность квадратов в скобках второго слагаемого, используя формулы сокращенного умножения:
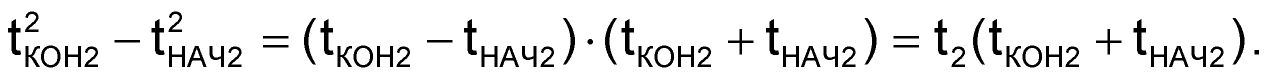 | (71) |
Теперь, после всех сокращений, формула (70) принимает вид:
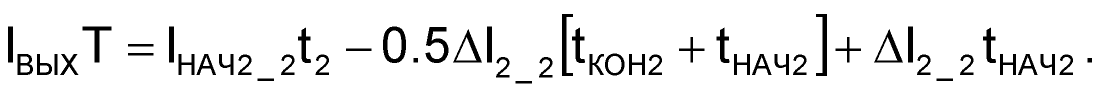 | (72) |
Раскрывая скобки и складывая сомножители с одноименными коэффициентами (в данном случае – tНАЧ2), получим:
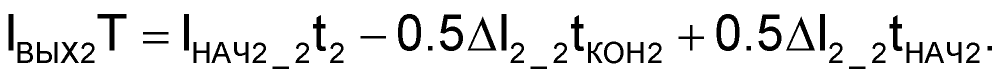 | (73) |
Вынося, в формуле (73) сомножитель –0.5ΔI2_2 за скобки, получим в итоге достаточно простую формулу, позволяющую выразить среднее значение выходного тока через параметры тока обмотки дросселя:
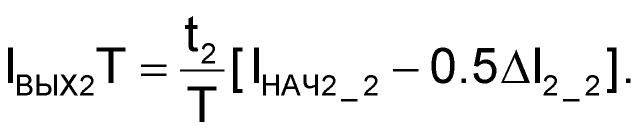 | (74) |
А это значит, что теперь мы можем определить один из трех недостающих параметров:
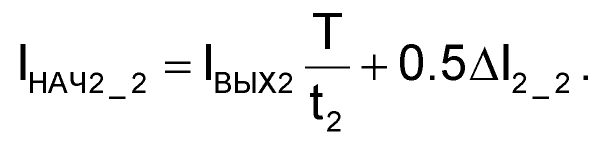 | (75) |
Когда у нас работает только второй канал, то ΔI2_2 = 2 А, поэтому ток обмотки W2 в начале второго интервала преобразования равен:
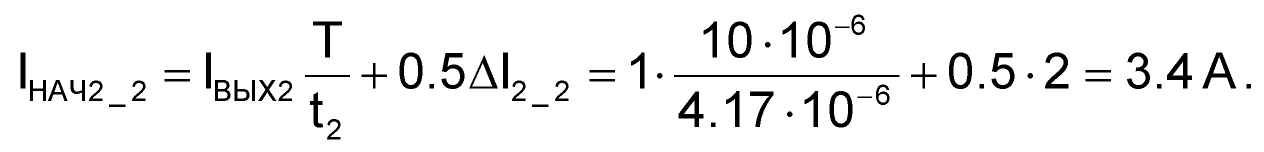 | (76) |
Если же работают оба канала (I2_2 = 1.53 А), тогда
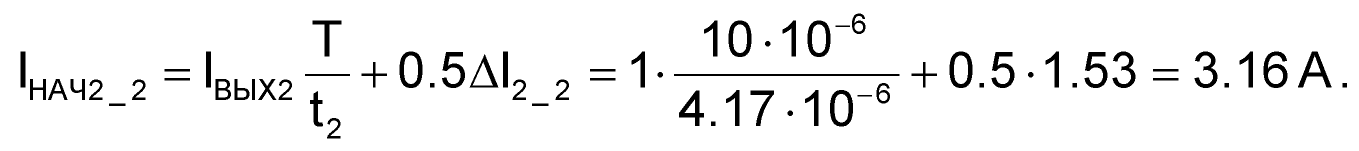 | (77) |
ООО «Мегател», ИНН 3666086782, ОГРН 1033600037020
Добавить свое объявление
* заполните обязательные данные
Статистика eFaster:
позиций 25 067 862
